Error using CatPhan504

Gustavo_Pamplona · January 29, 2026, 4:11pm

Dear pylinac team,

I’m new to pylinac and I’m trying to analyze dicom images of a catphan 504. Here’s the snippet:
from pathlib import Path
from pylinac import CatPhan504
cbct_folder = Path(“path/to/folder”)
mycbct = CatPhan504(cbct_folder)
mycbct.analyze()

But I get the following error message:

TypeError Traceback (most recent call last)
Cell In[40], line 1
----> 1 mycbct.analyze()

File ~\fss\fss\Lib\site-packages\pylinac\ct.py:2806, in CatPhanBase.analyze(self, hu_tolerance, scaling_tolerance, thickness_tolerance, low_contrast_tolerance, cnr_threshold, zip_after, contrast_method, visibility_threshold, thickness_slice_straddle, expected_hu_values, x_adjustment, y_adjustment, angle_adjustment, roi_size_factor, scaling_factor, origin_slice, roll_slice_offset)
2804 self.scaling_factor = scaling_factor
2805 self.roll_slice_offset = roll_slice_offset
→ 2806 self.localize(origin_slice)
2807 ctp404, offset = self._get_module(CTP404CP504, raise_empty=True)
2808 self.ctp404 = ctp404(
2809 self,
2810 offset=offset,
(…) 2816 expected_hu_values=expected_hu_values,
2817 )

File ~\fss\fss\Lib\site-packages\pylinac\ct.py:2356, in CatPhanBase.localize(self, origin_slice)
2354 def localize(self, origin_slice: int | None) → None:
2355 “”“Find the slice number of the catphan’s HU linearity module and roll angle”“”
→ 2356 self._phantom_center_func = self.find_phantom_axis()
2357 if origin_slice is not None:
2358 self.origin_slice = origin_slice

File ~\fss\fss\Lib\site-packages\pylinac\ct.py:2440, in CatPhanBase.find_phantom_axis(self)
2435 common_idxs = np.intersect1d(x_idxs, y_idxs)
2436 # fit to 1D polynomials; inspiration: https://stackoverflow.com/a/45351484
2437 # rcond should be explicitly passed. Started randomly failing in the pipe. v1.14.0 numpy release notes
2438 # say it should be explicitly passed. Value is arbitrary but small and tests pass.
2439 fit_zx = np.poly1d(
→ 2440 np.polyfit(zs[common_idxs], center_xs[common_idxs], deg=1, rcond=0.00001)
2441 )
2442 fit_zy = np.poly1d(
2443 np.polyfit(zs[common_idxs], center_ys[common_idxs], deg=1, rcond=0.00001)
2444 )
2445 return fit_zx, fit_zy

File ~\fss\fss\Lib\site-packages\numpy\lib_polynomial_impl.py:645, in polyfit(x, y, deg, rcond, full, w, cov)
643 raise TypeError(“expected 1D vector for x”)
644 if x.size == 0:
→ 645 raise TypeError(“expected non-empty vector for x”)
646 if y.ndim < 1 or y.ndim > 2:
647 raise TypeError(“expected 1D or 2D array for y”)

TypeError: expected non-empty vector for x

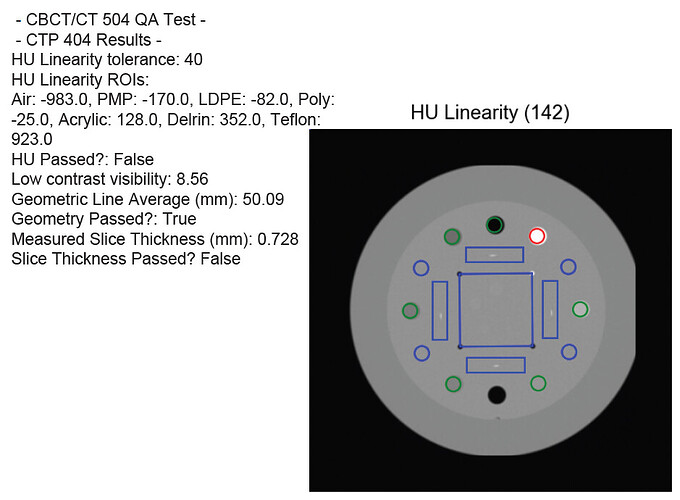
I know, as a matter of fact that the image is a bit clipped as it can be seen in the figure attached.
dicom_clipped

I was wondering if that’s really what is causing the error message, since the clipping doesn’t seem to be too much. Also, if that’s the case, if there’s any workaround for this issue.

I can also provide the dicom file if that’s useful. If the problem is not the clipping, which dicom parameters should I look at and correct?

Huge thanks and thanks in advance for your reply.

Best wishes,
Gustavo

alanphys · January 30, 2026, 11:11am

Hi Gustavo

The Catphan algorithm looks for the outline of the phantom in order to determine the relative positions of the structures inside. In your case it can’t find the outline or is determining it incorrectly because the phantom is clipped.

The simplest solution is to rescan the phantom with a larger field of view and make sure the phantom does not touch the sides of the scan.

Regards
Alan

Gustavo_Pamplona · January 30, 2026, 1:30pm

Hi Alan

Thanks for your quick reply. In the meantime, I sought to confirm that the issue was due to the clipping by creating an artificial image that was padded with some air-like values and rerunning pylinac analysis. This way, i was able to generate a report with this workaround:

But I considered that only as a way to determine the nature of the issue. Or would you say that the values in the report could be somewhat trusted? If so, any pitfalls that I should be aware of? If pylinac determine the relative position of the phantom structure, does it mean that the inferences will be in positions a bit displaced due to the clipping? (seems a bit the case from the figure)

Any feedback is highly appreciated. Thanks in advance!

Best wishes,
Gustavo